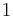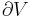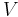Zeroth law of thermodynamics

Thermodynamics

Branches Classical · Statistical · Chemical Equilibrium / Non-equilibrium Thermofluids Laws Zeroth · First · Second · Third Systems State: Equation of state Ideal gas · Real gas Phase of matter · Equilibrium Control volume · Instruments Processes: Isobaric · Isochoric · Isothermal Adiabatic · Isentropic · Isenthalpic Quasistatic · Polytropic Free expansion Reversibility · Irreversibility Endoreversibility Cycles: Heat engines · Heat pumps Thermal efficiency System properties Property diagrams Intensive and extensive properties State functions: Temperature / Entropy (intro.) † Pressure / Volume † Chemical potential / Particle no. † († Conjugate variables) Vapor quality Reduced properties Process functions: Work · Heat Material properties Specific heat capacity  Compressibility  Thermal expansion  Property database Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Table of thermodynamic equations Potentials Free energy · Free entropy Internal energy Enthalpy Helmholtz free energy Gibbs free energy History and culture Philosophy: Entropy and time · Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics History: General · Heat · Entropy · Gas laws Perpetual motion Theories: Caloric theory · Vis viva Theory of heat Mechanical equivalent of heat Motive power Publications: "An Experimental Enquiry Concerning ... Heat" "On the Equilibrium of Heterogeneous Substances" "Reflections on the Motive Power of Fire" Timelines of: Thermodynamics · Heat engines Art: Maxwell's thermodynamic surface Education: Entropy as energy dispersal Scientists Daniel Bernoulli Sadi Carnot Benoît Paul Émile Clapeyron Rudolf Clausius Hermann von Helmholtz Julius Robert von Mayer William Rankine John Smeaton Georg Ernst Stahl Benjamin Thompson William Thomson John James Waterston

The zeroth law of thermodynamics is a generalization principle of the thermal equilibrium among bodies, or thermodynamic systems, in contact. It results from the definition and properties of temperature.^[1]

Contents 1 Zeroth law as equivalence relation 2 Thermal equilibrium between many systems 3 Temperature and the zeroth law 4 History 5 Notes 6 References

Zeroth law as equivalence relation

A system is said to be in thermal equilibrium when its temperature does not change over time. Let A, B, and C be distinct thermodynamic systems or bodies. The zeroth law of thermodynamics can then be expressed as:

"If A and C are each in thermal equilibrium with B, A is also in thermal equilibrium with C."

^[2]

The preceding sentence asserts that thermal equilibrium is a Euclidean relation between thermodynamic systems. If we also grant that all thermodynamic systems are (trivially) in thermal equilibrium with themselves, then thermal equilibrium is also a reflexive relation. Relations that are both reflexive and Euclidean are equivalence relations. One consequence of this reasoning is that thermal equilibrium is a transitive relation between the temperature T of A, B, and C:

If T (A) = T(B)

And T (B) = T(C)

Then T (A) = T(C).

Thermal equilibrium between many systems

Many systems are said to be in equilibrium if the small, random exchanges (due to Brownian motion, for example) between them do not lead to a net change in the total energy summed over all systems. A simple example illustrates why the zeroth law is necessary to complete the equilibrium description.

Consider N systems in adiabatic isolation from the rest of the universe (i.e., no heat exchange is possible outside of these N systems), all of which have a constant volume and composition, and which can only exchange heat with one another.

The combined First and Second Laws relate the fluctuations in total energy, , to the temperature of the ith system, 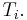and the entropy fluctuation in the ith system, 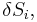as follows:

.

The adiabatic isolation of the system from the remaining universe requires that the total sum of the entropy fluctuations vanishes, or:

That is, entropy can only be exchanged between the N systems. This constraint can be used to rearrange the expression for the total energy fluctuation and obtain:

where is the temperature of any system j we may choose to single out among the N systems. Finally, equilibrium requires the total fluctuation in energy to vanish, in which case:

which can be thought of as the vanishing of the product of an antisymmetric matrix and a vector of entropy fluctuations 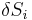. In order for a non-trivial solution to exist,

That is, the determinant of the matrix formed by must vanish for all choices of N. However, according to Jacobi's theorem, the determinant of a NxN antisymmetric matrix is always zero if N is odd, although for N even we find that all of the entries must vanish, , in order to obtain a vanishing determinant. Hence at equilibrium. This non-intuitive result means that an odd number of systems are always in equilibrium regardless of their temperatures and entropy fluctuations, while equality of temperatures is only required between an even number of systems to achieve equilibrium in the presence of entropy fluctuations.

The zeroth law solves this odd vs. even paradox, because it can readily be used to reduce an odd-numbered system to an even number by considering any three of the N systems and eliminating one by application of its principle, and hence reduce the problem to even N which subsequently leads to the same equilibrium condition that we expect in every case, i.e., . The same result applies to fluctuations in any extensive quantity, such as volume (yielding the equal pressure condition), or fluctuations in mass (leading to equality of chemical potentials). Hence the zeroth law has implications for a great deal more than temperature alone. In general, we see that the zeroth law breaks a certain kind of asymmetry present in the First and Second Laws.

Temperature and the zeroth law

It is often claimed, for instance by Max Planck in his influential textbook on thermodynamics, that the Zeroth law implies that we can define a "temperature function" or more informally, that we can "construct a thermometer."

In the space of thermodynamic parameters, zones of constant temperature will form a surface, which provides a natural order of nearby surfaces. It is then simple to construct a global temperature function that provides a continuous ordering of states. Note that the dimensionality of a surface of constant temperature is one less than the number of thermodynamic parameters (thus, for an ideal gas described with 3 thermodynamic parameters P, V and n, it is a 2 dimensional surface). The temperature so defined may indeed not look like the Celsius temperature scale, but it is a temperature function nonetheless.

For example, if two systems of ideal gas are in equilibrium, then P₁V₁/N₁ = P₂V₂/N₂ where P_i is the pressure in the ith system, V_i is the volume, and N_i is the "amount" (in moles, or simply the number of atoms) of gas.

The surface PV/N = const defines surfaces of equal temperature, and the obvious (but not only) way to label them is to define T so that PV/N = RT, where R is some constant. These systems can now be used as a thermometer to calibrate other systems.

History

The term zeroth law was coined by Ralph H. Fowler in the 1920s. This law is arguably the most fundamental of the four numbered laws of thermodynamics. It was called the zeroth law because the need to state it explicitly was not understood until after the First, Second, and Third Laws had been named and become commonplace.

Notes

1. ↑ Reif, F. (1965). "Chapter 3: Statistical Thermodynamics". Fundamentals of Statistical and Thermal Physics. New York: McGraw-Hill. pp. 102. ISBN 07-051800-9. 
2. ↑ Chris Vuille; Serway, Raymond A.; Faughn, Jerry S. (2009). College physics. Belmont, CA: Brooks/Cole, Cengage Learning. pp. 355. ISBN 0-495-38693-6. 

References

• Jos Uffink, J. van Dis, S. Muijs. Grondslagen van de Thermische en Statistische Fysica. Utrecht University
• Peter Atkins, "Four Laws That Drive the Universe."